All Construct with Tabulation
Updated: 01 February 2024
Problem
The same problem as the All Construct Memoization Problem but implemented using the tabular style in the previous problems
This is almost the same as the Count Construct solution but instead of incrementing the count we define the new running combination to reach a current position while retaining all other values that have reached that position thus far
For reference see the resulting array for a certain combination:
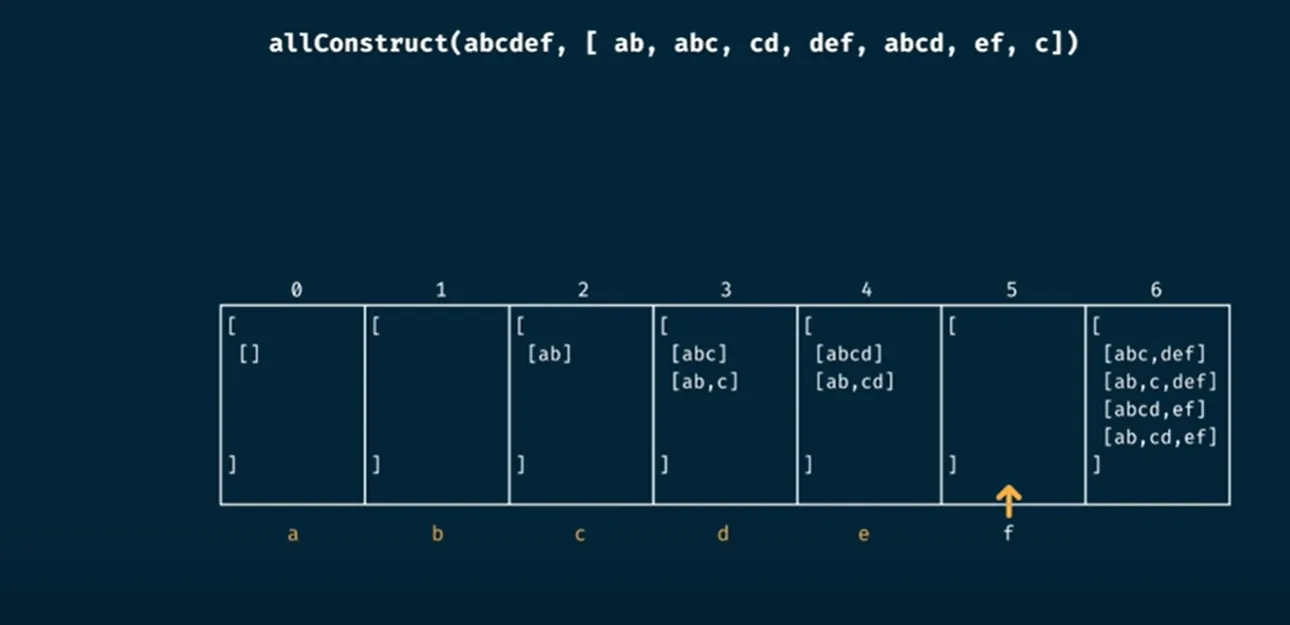
Tabulation Implementation
The implementation of this can be seen below:
1export const countConstruct = (target: string, subs: string[]): string[][] => {2 const table = new Array(target.length + 1)3 .fill(undefined)4 .map<string[][]>(() => []);5
6 table[0] = [[]];7
8 for (let index = 0; index <= target.length; index++) {9 const element = table[index];10 for (const sub of subs) {11 const fromIndex = target.slice(index);12 if (fromIndex.startsWith(sub)) {13 const nextIndex = index + sub.length;14 const newValues = element.map((el) => [...el, sub]);15
16 table[nextIndex].push(...newValues);17 }18 }19 }20
21 return table[target.length];22};In the above, the time complexity and space complexity . While the resulting complexity is pretty bad it is the best we’re going to get for this solution since it explicitly needs a list of all possible combinations