Grid Traveler with Tabulation
Updated: 01 February 2024
Problem
The same problem as the Grid Traveler problem
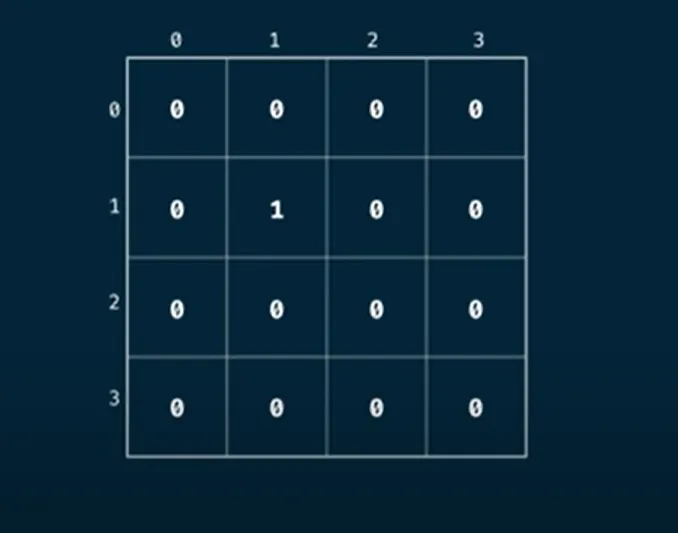
For this case, we will consider a table such that the last index is the desired size we want. Since we are doing a count we probably want to initialize the values of the table to 0 and 1 at position (1,1)
In terms of the size of our table we want to use (n+1, m+1) so that the last indexes are equal to the endpoints n and m, and also having a 0th index since a grid with length 0 is valid and needs to be considered
The initial table will look like this:
In the implementation here we will go through the grid and increment each valid move direction by the number of possible routes from the current position, this looks like so:
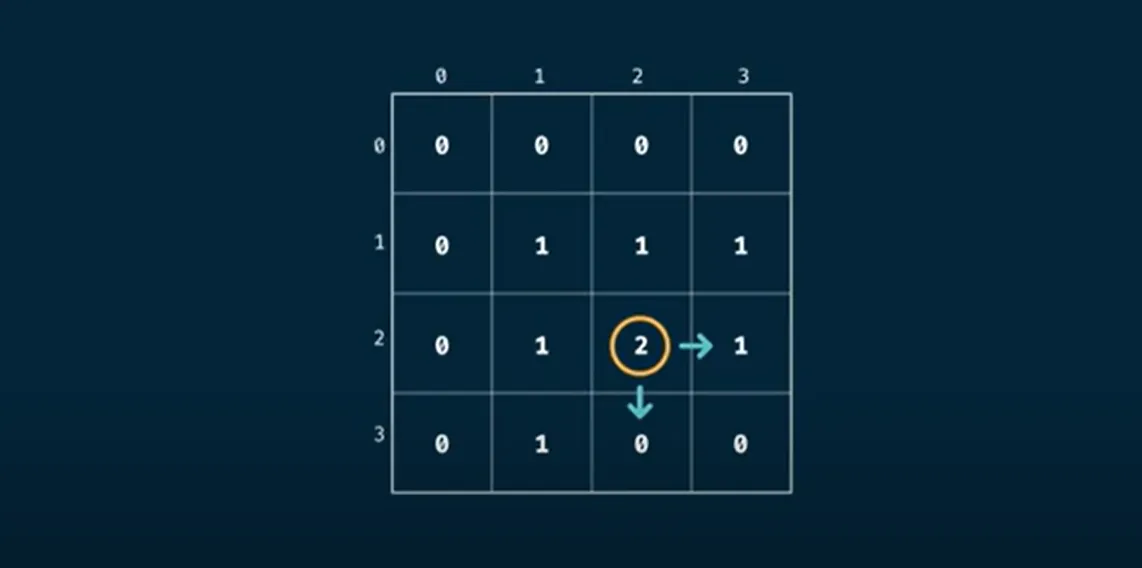
We can understand the fact that the top rows and columns are all 0 and will never change as when we are in a 0xn or mx0 grid there will be 0 ways to move to the end from that position
Tabulation Implementation
For our implementation we will define a table that has a position for each value we want. For our starting seed we will define an array of 0s and a 1 at index 1, from here we will step through each item and add it to the following two items. This is a bit of a different perspective on the Fibonacci problem than in the Recursive Fibonacci example
1export const gridTraveler = (m: number, n: number): number => {2 const table = new Array(m + 1)3 .fill(undefined)4 .map(() => new Array<number>(n + 1).fill(0));5
6 table[1][1] = 1;7
8 for (let indexM = 0; indexM <= m; indexM++) {9 for (let indexN = 0; indexN <= n; indexN++) {10 const element = table[indexM][indexN];11
12 if (indexM < m) table[indexM + 1][indexN] += element;13 if (indexN < n) table[indexM][indexN + 1] += element;14 }15 }16
17 return table[m][n];18};In this implementation we have a linear solution with time complexity and space complexity of