How Sum

Updated: 01 February 2024

Problem

Given a list of numbers write a function that will return the numbers from the array that can be summed to the given input if it is possible to sum the numbers to a given target, else return null. Each number can be used multiple times if needed. Can assume all numbers are positive

Some examples to consider:

1
canSum(7, [5,3,2,7]) = [2,5]
2
canSum(7, [2,4]) = null

We can follow a similar strategy as in the Can Sum example but here we will return an array of the values that added up the the desired result

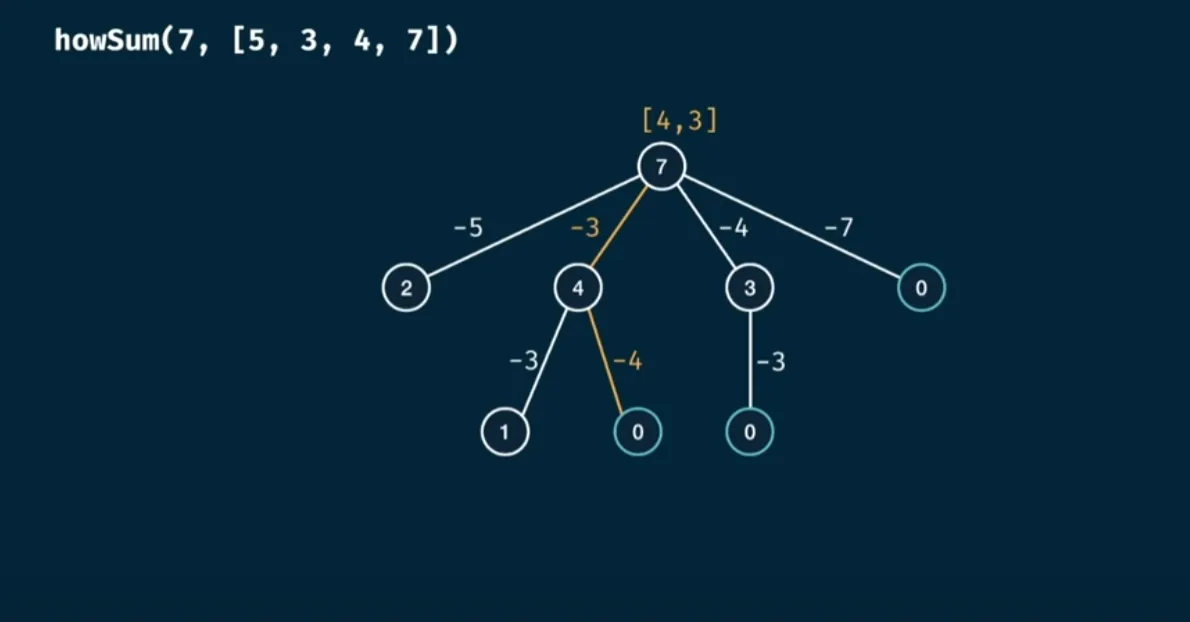
Base Implementation

The brute force solution looks like this:

dynamic-programming/memoization/how-sum.ts
1
export const howSum = (target: number, nums: number[]): number[] | null => {
2
  if (target == 0) return [];
3
  if (target < 0) return null;
4


5
  for (const num of nums) {
6
    const remainder = target - num;
7
    const result = howSum(remainder, nums);
8


9
    if (result) return [...result, num];
10
  }
11


12
  return null;
13
};

The above solution has a resulting time complexity of O(nm∗m)O(n^m * m) with nn as the target and mm as the length of the array. We can technically also consider the result array which is O(m)O(m) but that’s not very

With memoization

In the context of this problem we have cases in which the canSum function is being called with parameters that it has seen previously, we can apply the memoization as in other cases using this method

dynamic-programming/memoization/how-sum-memo.ts
1
type Memo = Record<number, number[] | null>;
2


3
export const howSum = (
4
  target: number,
5
  nums: number[],
6
  memo: Memo = {}
7
): number[] | null => {
8
  if (target in memo) return memo[target];
9


10
  if (target == 0) return [];
11
  if (target < 0) return null;
12


13
  for (const num of nums) {
14
    const remainder = target - num;
15
    const remainderSum = howSum(remainder, nums, memo);
16


17
    if (remainderSum) {
18
      const returnValue = [...remainderSum, num];
19
      memo[target] = returnValue;
20


21
      return returnValue;
22
    }
23
  }
24


25
  memo[target] = null;
26
  return null;
27
};

In the resulting implementation the resulting complexity is O(n∗m2)O(n * m^2) for time and O(m2)O(m^2) for space as we are now storing the result of each subcomputation to lookup later