Can Sum

Updated: 01 February 2024

Problem

Given a list of numbers write a function that will return if it is possible to sum the numbers to a given target. Each number can be used multiple times if needed. Can assume all numbers are positive

Some examples to consider:

1
canSum(7, [5,3,4,7]) = true
2
canSum(7, [2,4]) = false

We can visualize the case where we try to check if we can reach the value with each number in our input by subtracting them from some input value, we can look at if there are any options that we can use that will result in our sum possibly working, we can do this by checking if we become close to the result sum by subtracting this value and do this recursively. An explanation of the structure can be seen below:

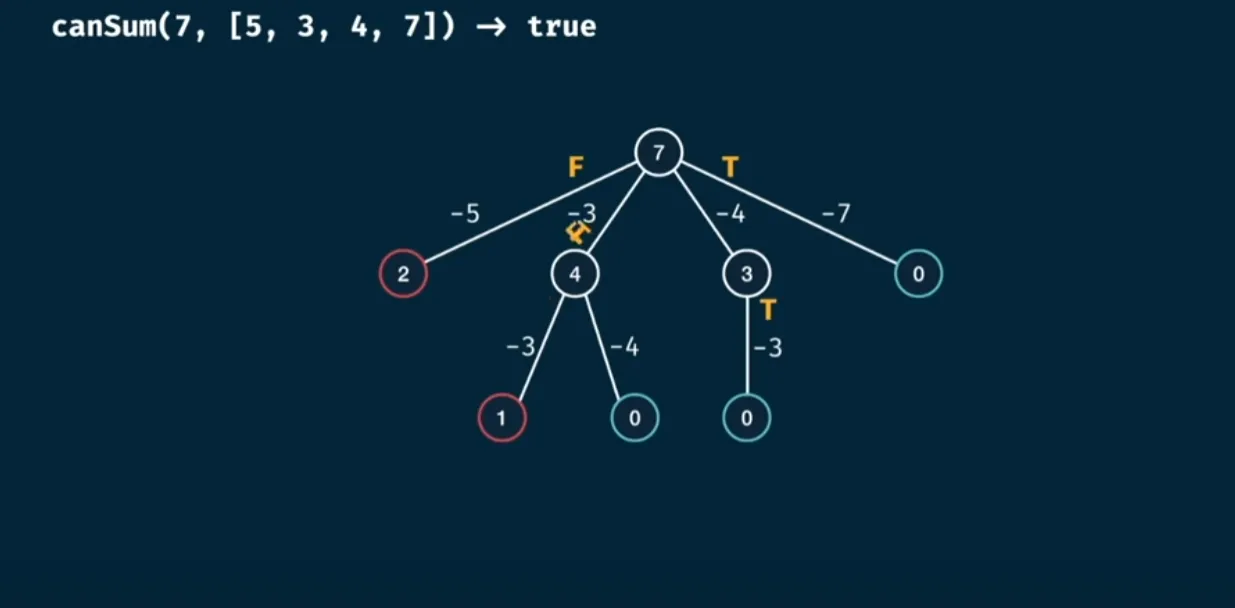
If we have any base case that returns true we can return all the way back up the tree

Base Implementation

The brute force solution looks like this:

dynamic-programming/memoization/can-sum.ts
1
export const canSum = (target: number, nums: number[]): boolean => {
2
  if (target === 0) return true;
3
  if (target < 0) return false;
4


5
  for (let num of nums) {
6
    const remainder = target - num;
7


8
    if (canSum(remainder, nums)) return true;
9
  }
10


11
  return false;
12
};

The problem with this solution is that it grows relatively quickly. Looking at the tree above the max height can be no higher than the target sum. In terms of branching we create a branch for each item in the array at each step, the time complexity of this then looks like O(nm)O(n^m) with nn as the target and mm as the length of the array

With memoization

In the context of this problem we have cases in which the canSum function is being called with parameters that it has seen previously, we can apply the memoization as in other cases using this method

dynamic-programming/memoization/can-sum-memo.ts
1
export const canSum = (
2
  target: number,
3
  nums: number[],
4
  memo: Record<number, boolean> = {}
5
): boolean => {
6
  if (target in memo) return memo[target];
7


8
  if (target === 0) return true;
9
  if (target < 0) return false;
10


11
  for (let num of nums) {
12
    const remainder = target - num;
13
    const result = canSum(remainder, nums, memo);
14


15
    if (result) {
16
      memo[target] = true;
17
      if (result) return true;
18
    }
19
  }
20


21
  memo[target] = false;
22
  return false;
23
};

In the resulting implementation the resulting complexity is O(m∗n)O(m*n) for time and O(m)O(m) for space