Grid Traveler Recursive Memoization

Updated: 01 February 2024

Problem

A traveler on a 2D grid begins in the top left and must travel to the bottom right corner by only moving down or right

How many ways can you travel to the goal on a grid that is m*n

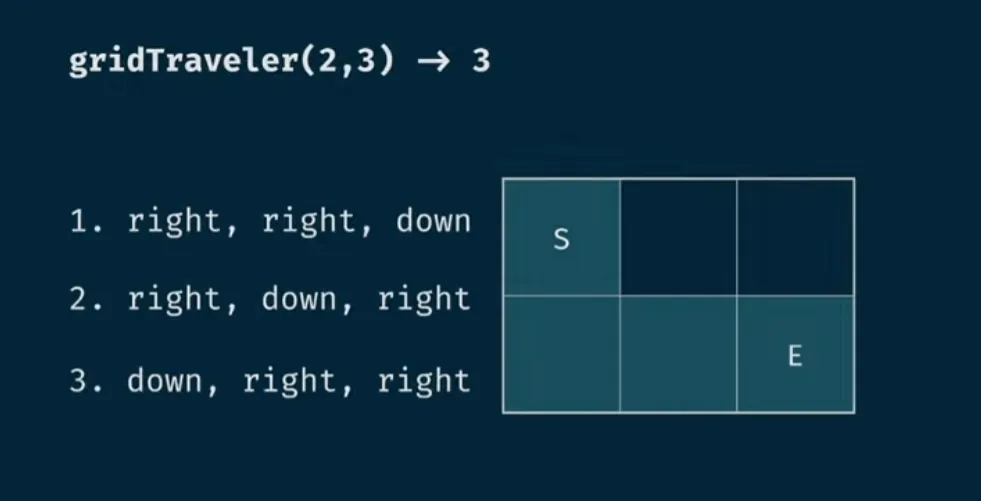
The resulting travel for a 2x3 grid may look like so:

Some special cases we want to ensure we can handle as well:

1
gridTraveler(1,1) = 1
2
gridTraveler(m,0) = 0
3
gridTraveler(0,n) = 0
4
gridTraveler(m,1) = 1
5
gridTraveler(1,n) = 0

Looking at the example, we can think about how any movement from a point in a grid shrinks the grid in some direction

From this idea we can see that the problem is somewhat recursive, we can visualize this problem as a tree that will look something like this:

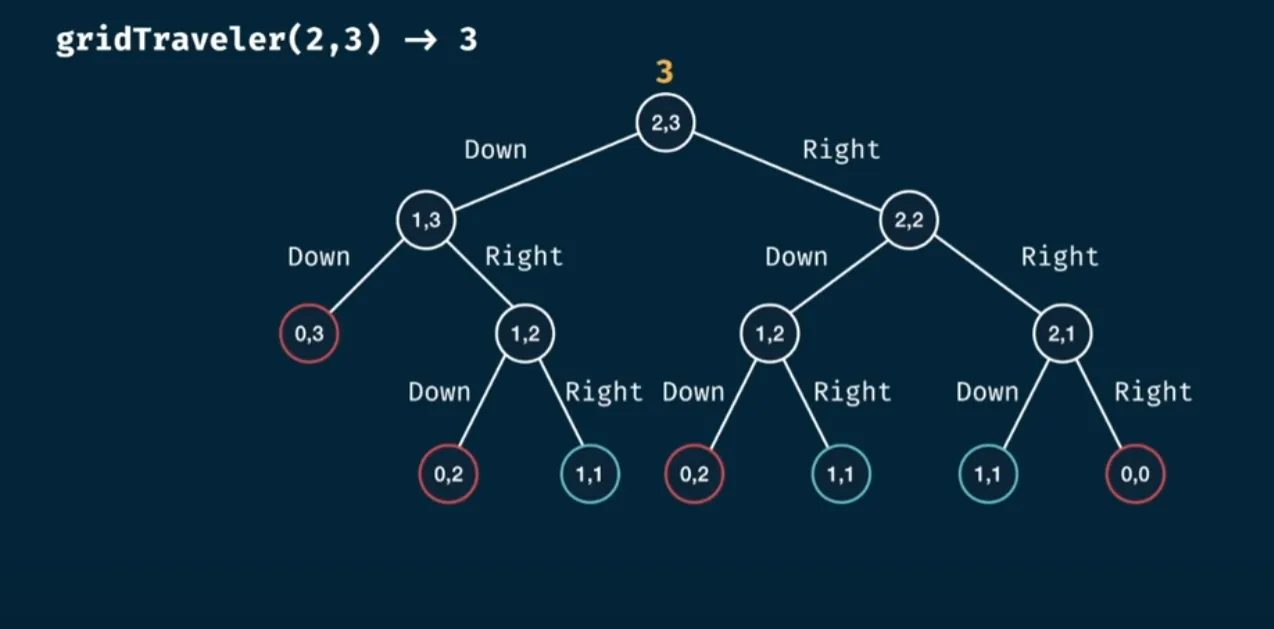
Any node that has a 0 or 1 can be considered the base case where we know the number of routes that can be travelled. Furthermore, we can also see that there are some repeated nodes

Base Implementation

1
export const gridTraveler = (m: number, n: number): number => {
2
  if (m == 1 && n == 1) return 1;
3
  if (m == 0 || n == 0) return 0;
4

5
  return gridTraveler(m - 1, n) + gridTraveler(m, n - 1);
6
};

This implementation starts to look a lot like the Fibonacci Implementation

In the tree for this implementation the time complexity will be $O(2^(m+n))$ and the space complexity is $O(n+m)$

With memoization

If we look at the tree we see that some subtrees are repeated directly, so we can try to memoize these.

1
const getKey = (m: number, n: number) => `${m},${n}`;
2

3
export const gridTraveler = (
4
  m: number,
5
  n: number,
6
  memo: Record<string, number> = {}
7
): number => {
8
  const key = getKey(m, n);
9

10
  if (key in memo) return memo[key];
11

12
  if (m == 1 && n == 1) return 1;
13
  if (m == 0 || n == 0) return 0;
14

15
  const result = gridTraveler(m - 1, n, memo) + gridTraveler(m, n - 1, memo);
16

17
  memo[key] = result;
18
  return result;
19
};

Thinking further about it we can consider that the number of solutions of 2,3 is the same as 3,2. We can also consider this for a further optimization but that is not implemented here