Fibonacci Recursive Memoization

Updated: 01 February 2024

Base Implementation

Looking at the recursive Fibonacci implementation below:

1
export const fib = (n: number): number => {
2
  if (n <= 2) return 1;
3
  return fib(n - 1) + fib(n - 1);
4
};

The time complexity is $O(2^n)$ and space complexity of $O(n)$

The above function gets extremely slow when n is large due to the recursive implementation. For example asking for fib(50) will have a time of $2^50$

If we visualize the implementation of the above function we will see a tree, for example for n=7:

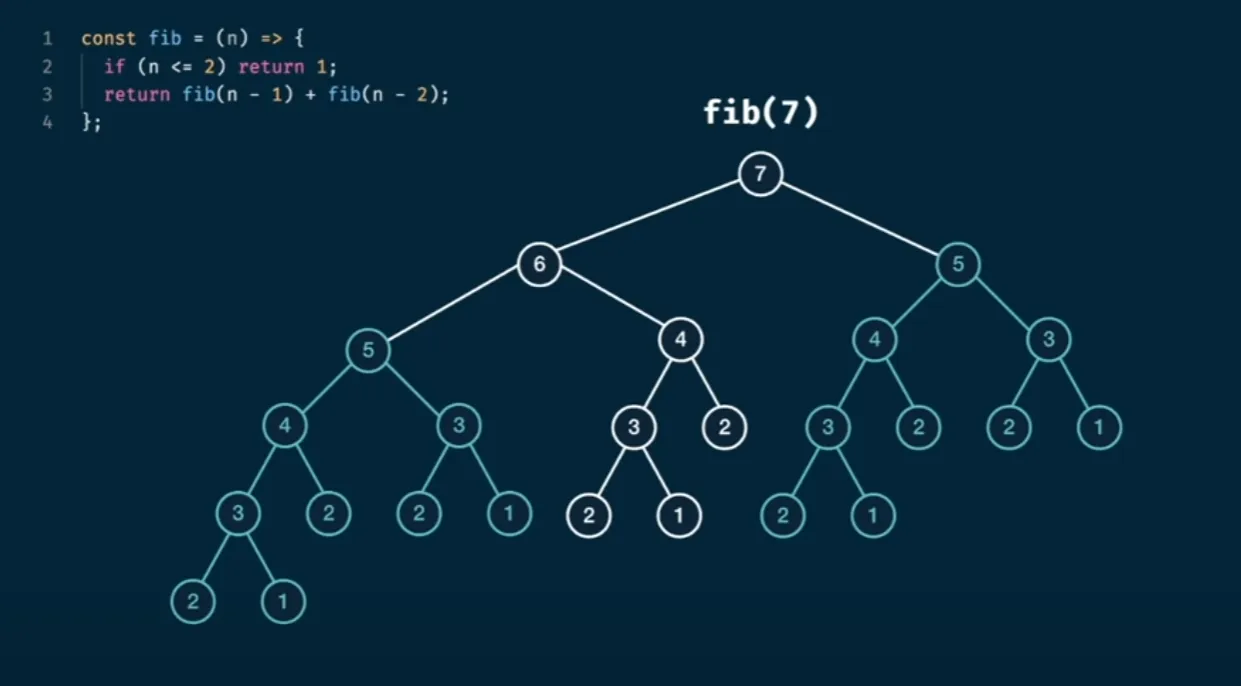
Looking at the subtrees we can see that there is a lot of data that is frequently recalculated and we can try to memoize this data

With Memoization

We can create a memo object that we pass around that will allow us to access and early escape a calculation

1
export const fib = (n: number, memo: Record<number, number> = {}): number => {
2
  if (n in memo) return memo[n];
3

4
  // rest of existing implementation with passing the memo
5
  if (n <= 2) return 1;
6
  const result = fib(n - 1, memo) + fib(n - 1, memo);
7

8
  // memoize the existing value and return it
9
  memo[n] = result;
10
  return result;
11
};

And now running fib(50) runs super quickly, this essentially takes the tree and collapses it into a more linear implementation and looks a bit like this:

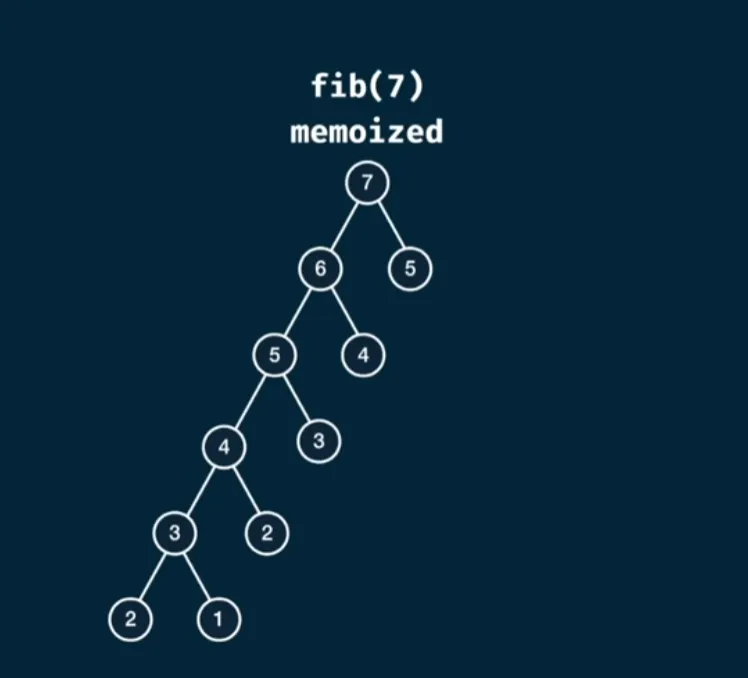
Based on this, the time complexity is now $O(n)$ without a relevant impact on the space complexity which is still $O(n)$